Therefore, at Coleridge, we teach maths differently. Children are not simply rushed through the curriculum, gaining vast, but superficial knowledge that can fall apart whenever they encounter something unfamiliar. Instead, significant time is spent ensuring children have a deep, sustained knowledge of mathematical concepts and that secure building blocks are in place before they are moved on.
Children are also taught to embrace the value of mistakes and false starts; to challenge each other’s thinking and to share what they ‘notice’, without fear of getting something wrong. In doing so, we have fostered ever positive attitudes in children who can think for themselves and persevere in the face of challenges.
To do all this, Coleridge has adopted a mastery approach to teaching maths. As a school, we are immensely proud that over the last few years, we have been able to work very closely with 2 in-school maths experts, both of whom have been trained by the NCETM as Mastery Specialists, to develop expertise in mastery pedagogy and embed excellent practice in our school. During this time, these specialists worked closely with a number of other schools to help them experience, experiment with, and implement ‘teach for mastery’ approaches within their own communities. Our mastery approach produces outstanding results, with a huge majority of our children making expected, or better than expected progress each year.
A Mastery Curriculum at Coleridge
At Coleridge, we have designed and planned our own programme of study in maths, using the National Curriculum, as well as materials produced by the NCETM and White Rose Maths, as a guide.
Taking full control of our curriculum has allowed us to ensure that every unit of works builds on previous learning, both within each year and in subsequent years, and that our core philosophy of maths teaching – that children learn how to think and solve creatively – remains at its heart.
Small Steps of Progression
Lessons do not simply serve to tick off a list of objectives from the national curriculum, one at a time. Instead, these objectives are seen as the end goal, with each unit taking into consideration how children will reach them; what small steps, what skills and knowledge will help the children achieve these goals? As a result, each unit of work is taught over several weeks, with topics being broken down into key skills which are carefully mapped out into a coherent, logical sequence. These small steps of progression allow children plenty of time to grasp and rehearse every concept and master each skill before they move on to the next.
Progression within a lesson also follows this same principle, with each part building on the previous. This allows as many children as possible to keep up with the learning and make sufficient progress.
Representations and Manipulatives
To achieve real mastery in maths – to become true mathematicians who can think mathematically – children need to develop two things: conceptual understanding and procedural fluency.
At Coleridge, a great deal of emphasis is placed on developing the former. The majority of ideas in maths are entirely abstract, generally characterised by a string of symbols that, without any understanding of what they signify, are simply meaningless. In order for children to attach meaning to these abstract ideas, we need to expose them to their structure.
Therefore, to help children construct a mental image of the maths, physical and visual resources are used in nearly all lessons. These are presented alongside abstract representations to allow children to continually make links between them. The teacher may vary which of these – concrete, pictorial or abstract – they focus on in a lesson, but children are exposed to all three, either sequentially or simultaneously. Teachers also ensure there is sufficient variation in the representations and examples that they use, as different representations of the same concept can be used to reveal more of the mathematical structure and in turn, deepen children’s understanding (more on this later).
Manipulatives are a key component in all children’s learning of maths; they are certainly not just reserved for those that are struggling. In fact, at Coleridge, teachers often require children to use manipulatives to prove they have a greater depth of understanding.
However, we strive to ensure that no child becomes entirely dependent on them, relying on them for the how, instead of the why. As soon as they are ready to do so, children are encouraged to visualise the resources instead, using drawings to help them if necessary, before eventually moving on to working wholly in the abstract.
Similar models, representations and resources are used from Reception, right up to Year 6, to ensure children consolidate their understanding and make links between different concepts.
For example, an array will be used from KS1 into the juniors to represent multiplication:

A tens frame, which starts as a fives frame in Reception, will be used in KS1 to represent small, whole numbers, but in upper KS2 to represent decimals:

Equal attention is given to developing children’s procedural fluency – their ability to use appropriate procedures accurately, flexibly and efficiently to solve a problem. Teachers at Coleridge ensure that children don’t simply learn facts and procedures off by heart, but instead understand the meaning and purpose behind them. In this way, we find that children make suitable and sensible choices when selecting a strategy to solve a problem.
Language
Mathematics requires children to talk like mathematicians, through the use of highly specialised and technical vocabulary. Therefore, teachers place huge emphasis on children being able to share their reasoning rather than just answers. All too often, however, children struggle to articulate even the most simple of thought processes clearly, commonly providing vague responses such as ‘I just knew it’ or ‘I worked it out in my head’. I once even had a child tell me ‘a ladybird’ had given them the answer! For this reason, teachers adopt a number of strategies to aid the development of children’s language, and in turn their reasoning skills:
- Stem sentences are often used alongside mathematical representations to reveal their structure or provide a generalisation. The ‘I say, you say…’ approach, where a stem sentence is first provided by the teacher but then copied by the class, is a way to get children to rehearse these ideas and, over time, make them more available to their own independent thinking.
- Teachers will often model their own thinking out loud to the class.
- Examples of other people’s reasoning will be discussed as a group.
- Relevant mathematical terminology is specifically taught and discussed.
- As well as strengthening conceptual understanding, manipulatives are used to provide a common language to talk about the maths. Teachers will encourage children to use these physical representations to structure their thinking and facilitate their explanations and reasoning.
- Thinking time and partner talk are used in every lesson.
Variation
To ensure that children gain a comprehensive understanding of each concept, teachers provide sufficient variation in the representations and examples that they give. The examples below, for instance, highlight the many ways in which the fraction ¼ can be presented:

Furthermore, teachers pay careful attention to the order in which they present questions to the children so that important features of a concept or strategy are emphasised.
For example:
120 – 90 = ___
122 – 92 = ___
119 – 89 = ___
Differentiation
A key principle of the mastery approach in maths is that children are taught as a whole class, with each child being given access to the same lesson content. Appropriate support is available for any child who might need it, and there are opportunities to deepen learning even further through the provision of more challenging activities. No assumptions are made before the lesson about which children might need more support, nor which ones will likely move on to the more difficult questions.
Tasks are carefully constructed so that, as children move through them, they become progressively more challenging and an appropriate level of scaffolding is provided at each stage to ensure that more children can access them and deepen their understanding. Open-ended tasks, which all children can access at their own level, are regularly used as well.
Lesson Design
Lessons will commonly be taught using a ‘ping pong’ style approach, so called because the teacher orchestrates a continual back-and-forth dialogue with the children, using questions, short tasks, explanations, demonstrations, and discussions. This enables the teacher to vary the pace and direction of the lesson if necessary, and to continuously monitor the progress of the whole class.
Talk partners and table groups are not fixed and teachers may vary how they organise their class depending on the requirements of the lesson.
Problem Solving and Reasoning
Skills teaching is of course essential, but a curriculum focussed solely on developing competence with number, without opportunities for rich problem solving, is akin to being taught scales on a piano but never learning to play music. Providing children with the skills required to solve mathematical problems in life should therefore be the principal aim of any maths curriculum. It is crucial that, in addition to teaching number skills and number fact, children are exposed to rich mathematical problems in every single lesson.
Therefore, at Coleridge, our children do not learn just how to ‘do maths’; huge emphasis is also placed on teaching them to ‘think mathematically’. Through contextualized problem solving activities and thought-provoking tasks, children work in the same way real mathematicians do, learning skills such as reasoning, conjecturing, generalizing and working systematically. This allows children to experience maths as something that is fundamentally useful, and not just a series of skills that must be learnt in order to pass tests.
Maths in the EYFS
Our EYFS maths curriculum is designed to ensure that, throughout the year, all children develop a secure foundation in the six key areas of early mathematical understanding: pattern, measure, shape and space, cardinality and counting, comparison, and composition. We also ensure our children are exposed to, and feel secure in, the five principles of counting: the one-to-one principle, the stable order principle, the cardinal principle, the abstraction principle, and the order irrelevance principle.
Each week, there is a maths focus in the classroom and children will be able to access the carefully-planned-for activities within the continuous provision to develop their understanding of the week’s focus. These activities might include games in the outdoor provision, craft activities, or role play scenarios. The children will also participate in active and engaging whole class sessions throughout the week, designed to expose them to key mathematical concepts, and illustrate important mathematical language.
In addition to this, teachers ensure that key mathematical learning is drawn out, where possible, from other areas of the curriculum too, such as from key texts they are reading, artists they are studying, or science activities they are discussing. Maths also forms part of the children’s everyday routines, for example, using the ‘Tens Frame’ register, singing maths songs, and counting resources during tidy up time.
We know that developing a mathematical vocabulary in the early years is vital to children being able to access the maths curriculum in Year 1 and beyond. EYFS staff encourage children to use the vocabulary they have been learning in whole class sessions throughout the day in their play. We know that when children use mathematical language in a way that feels relevant to them and their experiences, they are more likely to retain it.
At Coleridge, we believe that children’s early experiences of maths in school should be interesting, fun, challenging and exciting. We want children to spot patterns, ask questions, make suggestions, and to think like mathematicians from the very start.
Catch Up and Keep Up
Teachers at Coleridge have high expectations for all children and firmly believe that every single one can succeed in this subject, that no child ‘just can’t do it’. Lessons are carefully planned to take into account common misconceptions and particularly difficult concepts, ensuring that all children can access the lesson content, either through skilled questioning, supportive scaffolding or appropriate resourcing.
Using various assessment for learning strategies, teachers also have the skills to quickly adapt lessons, as well as sequences of lessons, to address the needs of their children. Additional steps may be added, or the pace of a lesson adjusted, to ensure that they continue to firm up the foundations of their knowledge and understanding, and nurture their love for the subject.
Despite a teacher’s best efforts, however, some children may still struggle with a particular concept. These children are quickly identified and extra support or intervention is put in place to help them keep up.
Coleridge has a team of intervention support staff who are trained to deliver a number of maths interventions:
- Becoming First Class at Number
- First Class at Number (1 and 2)
- Talk for Number
- Success at Arithmetic
- Number Champions
Marking and Feedback
The most successful form of marking and feedback is that which the children receive instantly. Where possible, therefore, lessons are designed so that immediate feedback to an activity can be given through class discussion. For activities where instant feedback is not possible, children are provided with answer sheets so that they can mark their own work. They are encouraged to do so honestly and overtime, learn how to evaluate their own learning by identifying for themselves where they might need more support.
Teachers will always review the children’s work at the end of a lesson, using it to help inform their planning of the next. A distinction, however, is drawn between errors that arise from misconceptions, and those that are considered accidental mistakes.
RedStart – A Financial Education
Coleridge has partnered up with the charity RedSTART to deliver the ‘Changing the Game’ programme to all children in Years 2 to 6 in the Spring and Summer terms. The programme involves fun and interactive workshops which provide children with a fantastic financial education. We are really excited about what the children will learn and the great life skills it will leave them with. To find out more about this programme, and to see the specific learning objectives for each year group, please see the RedStart Overview below or check out the RedStart website.
From the perspective of a Mastery Specialist
Support Documents For Your Child
In this section of the website, you will find a series of documents that will help you support your child at home in different areas of the maths curriculum. Each document provides information about what your child needs to know, and then suggests activities, games and websites that will help develop their skills.
Developing Fluency with Number and Mental Calculation
What Do Children Need to Know and Why?
We are regularly approached by parents, seeking advice on ways they can support their child at home with maths. Answering this question can be difficult as this subject is made up of many different topic areas and children will have varying degrees of understanding in each one.
However, learning maths is like building a tower; children must have firm foundations and acquire specific building blocks in a certain order. If any of these blocks of understanding are missing, then the tower is shaky and can be toppled with the presentation of new challenges or concepts later down the line. The most important job that parents can do at home, therefore, is to make sure that these basic building blocks are secure.
The purpose of this section is to explain what these basic skills are – to make clear the steps which children progress through as they develop an early understanding of number. If parents understand this progression for themselves, then they are better placed to identify any gaps in their child’s learning and, more importantly, will know what to do to fill them.
Developing a Conceptual Understanding of Number
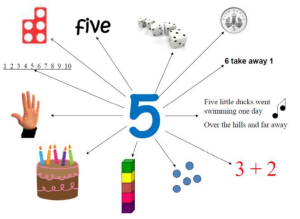
A key priority of any primary school teacher is to ensure that children develop a strong sense of number and place value. Children will continually encounter numbers in the world around them, whether it be on the bus they took to school or on their front door at home. But the ability to recognise the symbol 5 and name it, is very different from understanding the ‘fiveness’ of it (i.e. that it represents 5 things). It is the development of this latter skill that is crucial to a child’s mathematical ability.

Furthermore, it is important to recognise that just because a child can count (i.e. recite number names in order), they do not necessarily have any understanding of what these words mean. As with learning the alphabet or a favourite nursery rhyme, children can recall a sequence of numbers or words by rote, without any real grasp or understanding of what they are saying (hence why young children often omit numbers as they count). Gaining familiarity with number names through songs and rhymes is of course helpful, but emphasis should be placed on enabling children to make links between these symbols, their names and the number of objects they equate to.
If, for instance, I presented you, as an adult, with the calculation below, my guess would be that you couldn’t do it:

You might be able to say it as a sentence, ‘apple plus bee’, but without an appropriate conceptual understanding of these symbols, any effort to solve the equation would be futile. This is no different from asking a child, who has not yet linked the abstract numerals (e.g. 4, 0, 2 etc) in our number system with anything tangible (i.e. they don’t yet know that 3 relates to 3 things), to add together 4 and 3. It is only once a meaning has been attributed to these symbols (if I told you that ![]() = 5 and
= 5 and ![]() = 2, could you do it now?) that children can solve simple arithmetic calculations.
= 2, could you do it now?) that children can solve simple arithmetic calculations.
In order for children to cultivate this number sense, various resources (such as counters, multi-link and Numicon) are used to expose their structure, enabling children to develop mental representations of what they look like. Much of a child’s early experience with number will involve physical, movable objects which they can manipulate to suit the task in hand. Over time, as a child’s conceptual understanding develops, these concrete objects will be replaced with pictures and then simply with mental images. Eventually, children will feel secure enough in their understanding to work wholly in the abstract.
Addition and Subtraction Facts to 20
Once children have grasped the concept of number, the focus turns to developing their knowledge of addition and subtraction facts within 20. These serve as the building blocks for additive calculation, in much the same way that times tables provide the foundations for multiplication and division. For instance, when children are presented with calculations, such as 46 + 52 = ?, they must be able to automatically retrieve the simple arithmetic facts they need in order to solve it fluently and efficiently (in this case, 6 + 2 = 8, and 4 + 5 = 9, therefore 40 + 50 = 90).
If they can’t retrieve this knowledge, if instead their working memory is required to calculate these basic facts on the spot, then children can get overloaded with information and become confused, and hence find themselves unable to focus on the ‘bigger ideas’ in hand. Imagine another example, whereby the purpose of the lesson is on finding change from a specified amount of money, and a child is working on a problem which involves the calculation: £10.00 – £7.23. Without a quick recall of key addition and subtraction facts, the child’s attention deviates from the intended learning (about change) and instead focuses on calculating simple facts, most likely using inefficient strategies such as counting on their fingers. If, during a lesson, a child is regularly having to digress from the mathematical concept being taught and compute facts that he/she should already know, it is not hard to see how, and why, children end up struggling to take on board new information.
Mental Calculation Strategies
An ability to think mathematically is not solely about finding the right answer to a problem; it also involves choosing the most efficient method of doing so. At primary school, a great deal of emphasis is placed on developing children’s formal methods of calculation, with children learning how to apply them from Year 3 upwards. As soon as children become familiar with these strategies however, they have a tendency to use them over any other, often forgoing quicker, more suitable mental maths strategies. For example, the formal method of subtraction will certainly help you find the correct answer to 102 – 99, but a child who recognises that they can quickly find the difference between these two numbers in their head instead (by counting on 3) displays a much higher level of thinking. Therefore, when teaching children calculation strategies, considerable attention is also paid to helping them identify which strategies to use and when. The documents that follow provide you with ideas of games and activities you can play at home to help you support your child’s learning of these key mathematical skills (a secure sense of number, quick recall of number facts, and an ability to select and use the most appropriate mental calculation strategy).
Knowing Numbers to 20
A Child’s First Introduction to Number
When exposing children to the numbers 1 to 10, in order to create an in depth understanding of what they are and what they represent, it is vital that they experience each one in all its guises. That is, that they encounter the numbers in the various different forms they pertain to. The number 5, for example, represents 5 things, and there are endless opportunities in the world around us to reveal this structure to children.

But this is by no means a complete picture of the number 5. The 5 on a clock, for instance, does not denote 5 things, nor does the 5 on my front door necessarily mean I have 5 of them! This is because numbers are also used to put things in order and the knowledge that 5 comes after 4, but before 6, is equally important to understand. Therefore, this aspect of number must also be regularly exposed to the children so that they are able to, for example, locate the correct page in a book, look up a date in the calendar, or know how old they will be next year.
Below is a list of simple activities that can be carried out at home, or on the way to school, to help your child grasp these different concepts of number:
- Count sets of 5 things at home, or outside.
- Encourage your child to spot the number 5 whenever you are out and about.
- Tell your child to show you 5 fingers whenever they want your attention at home.
- Write down some numbers and ask them to point out the number 5.
- Get them to locate page 5 in a book.
- Can they then find a word with 5 letters?
- Tell your child to count as they go up 5 stairs. Are they able to count backwards as they come down again? You could do this with paving stones too.
- Ask them to draw a set of 5 dots in lots of different arrangements.
- Get them to draw a monster with 5 heads, 5 legs and 5 tails.
Teen Numbers
Our number system, for the most part anyway, follows a very repetitive structure and a secure knowledge of tens, hundreds, thousands etc., and the pattern they follow, would enable you, if you had to, to continue counting on and on, into infinity. However, the numbers 11 to 19, or the ‘teen numbers’ as they are commonly referred to, do not follow this structure and have instead been assigned an arbitrary collection of names – ones which don’t appear to follow any recognisable pattern. It is for this reason that much more time must be dedicated to helping children familiarise themselves with the teen numbers and their associated structures and names. Common errors to look out for include confusing the names twenty and twelve, reciting the names in the wrong order, or omitting some altogether, or recording them incorrectly based on how they are said (e.g. sixteen written as 61). Children should also be corrected if they say, for example, that the number eleven is a 1 and a 1, and discussions should be had about the first 1 actually being a ten.
Concrete Resources
Several physical resources are used to help children learn the ‘shape’ of numbers. Numicon, which children are introduced to as soon as they start school, is ideal for this purpose as the way in which it presents numbers immediately highlights many of their properties. For instance, children can visually see their relative size, and use them to identify which numbers are one more, or one less, than another. The concept of odd and even is also very apparent.

But another key feature of this resource is its ability to draw attention to the component parts of a number. There is an expectation that children will know all of their number bonds within 20 by the end of Year 2 (e.g. that 5 = 0 + 5 = 1 + 4 = 2 + 3 = 3 + 2 = 4 + 1 = 5 + 0) and familiarity with Numicon can really help embed this knowledge.
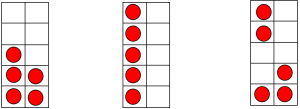
The pictures below show some of the different ways we can make the numbers 6 and 7:

However, Numicon is not the only effective model and image for mathematics and several other resources are used in the classroom as well, not least to ensure children don’t just think that numbers come in the shape (and colour!) that are represented by Numicon. Bead strings, particularly with their purposeful use of colour, also create a visual image of number, as do trains of multilink cubes, or the slightly more abstract Cuisenaire Rods.

The five and ten frames, easily replicable rectangular frames used alongside counters or objects, illustrate essential characteristics of numbers too.
Below, the five frame is being used to demonstrate important aspects of the number 4: that it is made of 1 and 3 or 2 and 2, that it is one less than 5, and that it is still the same number, even if the objects move position.

The examples of the ten frame here all show something different about the number 5 too.
Unlike Numicon, this resource also makes apparent a number’s relationship to the number 10.
Many concrete materials are used to emphasise the central feature of teen numbers too – that they are composed of a ten and a ones number.

Subitising
Subitising is the ability to instantly recognise the number of objects in a small group, without counting them. Most adults can subitise up to 5 objects; for sets of items beyond that, we tend to break them up into smaller groups (perhaps seeing two sets of 3 for a group of 6 objects). When cultivating a sense of number in children’s early years of school, it is essential that they are given plenty of opportunity to develop this skill of subitising. The resources above, particularly the five and ten frame, are an ideal way to do this.
But before you delve into the list of activities below, which have been provided to help you develop your child’s number sense, it is important that you bear in mind the following: although these resources are a brilliant way of enabling your child to visualise the maths, we need to ensure they don’t become over reliant on them. That is, that they are so dependent on the apparatus that they are unable to do the maths without them. In order to prevent this, we must at some point encourage children to picture the resources mentally instead. Eventually they should get to the point where they no longer require them at all.
Activities and Games
- Use a feely bag with Numicon to describe a secret number. ‘It has four holes down one side and a bit that sticks out at the end. What number is it?’ You could swap roles with your child too and encourage them to describe the shape instead.
- Get your child to close their eyes and then pass them a Numicon shape or a Cuisenaire rod. Without looking, they must say what number it is. Alternatively, they can show you the shape they have felt using counters. This is a great way to encourage visualisation.
- Place the Numicon pieces, or Cuisenaire rods, in order and then hide one. Which one is missing?
- Ask children to make a particular Numicon shape using counters.
- Can you use the bead string to show me a number that is one less than 13? Or could you draw what the bead string would look like?
- Make pictures using only odd or even numbers.

- Give children a handful of objects which they must arrange into a five or ten frame to see how many there are. They could estimate the number first, but they should not count them.
- Repeat the activity above, but without the frame. Can children say how many objects there are without counting? Can they explain how they know?
- Bake some cakes in the shape of Numicon.

- Say a number orally, or show it using digits. Get your child to make this number using one of the resources, such as a ten frame, or with a bead string. Focus particularly on ‘teen’ numbers.
- Make, and then play, a matching game, where players have to find a number in digits, words and the ten frame shape.
- Show your child a Numicon shape or a number using the Cuisenaire rods or on a bead string; they must write down what it is in numerals.
- Use a pile of socks to get your child to help you decide whether you have an odd or even number. Can they find all the odd/even numbers up to 20? How do they know if a number is odd or even?
- Put all of the Numicon shapes in a feely bag. Challenge your child to pull out all of the odd/even numbers without looking. To make this activity more challenging, try it with Cuisenaire rods.
- Choose any number between 10 and 20 and ask your child to count from this number up to 20 and then back again. Counting backwards can be particularly difficult.
- Board games, notably those that use number tracks such as Snakes and Ladders, are great for early number recognition and counting too.
This is certainly not an exhaustive list of activities, and many more ideas can be found by searching online. You may even find you have the confidence to create some of your own!
Calculation Policy
Key Stage 1
Lower Key Stage 2
Upper Key Stage 2
The Maths Curriculum
Please refer to the curriculum maps below to find out when topics are taught in each year group.
You can then see the specific learning objectives they are taught in each unit below:
Place Value
Year 1:
- Can read and write numbers to 20 in numerals and words.
- Can read and write numbers to 100 in numerals.
- Can count forwards and backwards to 100 from any given number.
- Can count in 2s, 5s and 10s up to 100.
- Can identify one more and one less than a given number up to 100.
- Can recognise odd and even numbers.
- Can identify and represent numbers using objects and pictorial representations, including the ten frame and number line.
- Can use the language of: equal to, more than, less than (fewer), most, least.
Year 2:
- Can read and write numbers to at least 100 in numerals and in words.
- Can recognise the place value of each digit in a 2-digit number (tens, ones).
- Can identify, represent and estimate numbers using different representations, including the number line.
- Can partition 2-digit numbers into different combinations of tens and ones (e.g. 23 is the same as 2 tens and 3 ones which is the same as 1 ten and 13 ones)
- Can compare and order numbers from 0 up to 100.
- Can use <, > and = signs.
- Can count in steps of 2, 3 or 5 from 0, forward or backward.
- Can count in steps of ten from any number, forward or backward.
- Can use counting in steps to help them solve problems.
- Can use place value and number facts to solve problems.
Year 3:
- Can read and write numbers up to 1000 in numerals and in words.
- Can recognise the place value of each digit in a 3-digit number (hundreds, tens, ones.)
- Can count from 0 in multiples of, 4, 8, 50 and 100.
- Can find 10 or 100 more or less than a given number.
- Can compare and order numbers up to 1000.
- Can identify, represent and estimate numbers using different representations.
- Can solve number problems and practical problems involving these ideas.
Year 4:
- Can count in multiples of 6, 7, 9, 25 and 1000.
- Can find 1000 more or less than a given number.
- Can count backwards through zero to include negative numbers.
- Can recognise the place value of each digit in a 4-digit number (thousands, hundreds, tens, and ones).
- Can order and compare numbers beyond 1000.
- Can identify, represent and estimate numbers using different representations.
- Can round any number to the nearest 10, 100 or 1000.
- Can solve number and practical problems that involve all of the above and with increasingly large positive numbers.
- Can read Roman numerals to 100 (I to C) and know that over time, the numeral system changed to include the concept of zero and place value.
Year 5:
- Can read and write numbers to at least 1 000 000 and determine the value of each digit.
- Can order and compare numbers to at least 1 000 000.
- Can count forwards or backwards in steps of powers of 10 for any given number up to 1 000 000.
- Can interpret negative numbers in context, and count forwards and backwards with positive and negative whole numbers through zero.
- Can round any number up to 1 000 000 to the nearest 10, 100, 1000, 10 000 and 100 000.
- Can solve number problems and practical problems that involve all of the above.
- Can read Roman numerals to 1000 (M) and recognise years written in Roman numerals.
Year 6:
- Can read and write numbers up to 10 000 000 and determine the value of each digit.
- Can order and compare numbers up to 10 000 000 and determine the value of each digit.
- Can round any whole number to a required degree of accuracy.
- Can use negative numbers in context, and calculate intervals across zero.
- Can solve number and practical problems that involve all of the above.
Addition and Subtraction
Year 1:
- Can read, write and interpret mathematical statements, involving addition (+), subtraction (-) and equals (=) signs.
- Can represent and use number bonds and related subtraction facts within 20.
- Can add and subtract one-digit and two-digit numbers within 20, including zero, using various strategies.
- Can solve one-step problems that involve addition or subtraction, using concrete objects or using pictorial representations such as a number line.
- Can solve missing number problems, such as 7 = ? – 9.
Year 2:
- Can solve problems with addition and subtraction using concrete objects and pictorial representations, including those involving numbers, quantities and measures.
- Can solve problems with addition and subtraction, applying their increasing knowledge of mental and written methods.
- Can recall and use addition and subtraction facts to 20 fluently.
- Can derive and use related facts up to 100 (e.g. if I know 5 – 3 = 2, then I also know that 50 – 30 = 20.)
- Can add and subtract a 2-digit number and ones or tens, using concrete objects, pictorial representations, such as a number line, or mentally.
- Can add two 2-digit numbers, using concrete objects, pictorial representations such as a number line, or mentally.
- Can subtract two 2-digit numbers, where no regrouping is required (e.g. 74 − 33), using concrete objects, pictorial representations such as a number line, or mentally.
- Can subtract two 2-digit numbers, where regrouping is required (e.g. 52 − 27; 91 – 73), using concrete objects, pictorial representations such as a number line, or mentally.
- Can add three 1-digit numbers.
- Can show that addition of two numbers can be done in any order (commutative) and subtraction of one number from another cannot.
- Can recognise and use the inverse relationship between addition and subtraction and use this to check calculations.
- Can use estimation to check that the answer to a calculation is reasonable (e.g. knowing that 48 + 35 will be less than 100).
- Can solve missing number problems.
Year 3:
- Can add or subtract a 3-digit number and ones, tens or hundreds mentally.
- Can add numbers with up to three digits, using formal written methods of columnar addition.
- Can subtract numbers with up to three digits, using formal written methods of columnar subtraction.
- Can estimate the answer to a calculation and use inverse operations to check answers.
- Can solve problems using number facts, place value, and more complex addition and subtraction.
- Can solve missing number problems.
Year 4:
- Can add numbers with up to 4-digits using the formal written methods of column addition where appropriate.
- Can subtract numbers with up to 4-digits using the formal written methods of column subtraction where appropriate.
- Can estimate and use inverse operations to check answers to a calculation.
- Can solve addition and subtraction two-step problems in contexts, deciding which operations and methods to use and why.
Year 5:
- Can add and subtract whole numbers with more than 4-digits, including using formal written methods (columnar addition and subtraction).
- Can add and subtract numbers mentally with increasingly large numbers.
- Can use rounding to check answers to calculations and determine, in the context of a problem, levels of accuracy.
- Can solve addition and subtraction multi-step problems in contexts, deciding which operations and methods to use and why.
Year 6:
- Can perform mental calculations, including with mixed operations and large numbers.
- Can use their knowledge of the order of operations to carry out calculations involving the four operations.
- Can solve addition and subtraction multi-step problems in contexts, deciding which operations and methods to use and why.
- Can solve problems involving addition, subtraction, multiplication and division.
- Can use estimation to check answers to calculations and determine, in the context of a problem, levels of accuracy.
Multiplication and Division
Year 1:
- Can solve one-step problems involving multiplication, by calculating the answer using concrete objects, or pictorial representations and arrays, with the support of the teacher.
- Can solve one-step problems involving division, by calculating the answer using concrete objects, or pictorial representations and arrays, with the support of the teacher.
Year 2:
- Can recall and use multiplication and division facts for the 2, 5 and 10 times table and recognise the odd and even numbers within it.
- Can recall doubles and halves to 20.
- Can calculate mathematical statements for multiplication and division within the multiplication tables and write them using the multiplication (×),division (÷) and equals (=) signs.
- Can show that multiplication of two numbers can be done in any order (commutative) and division of one number by another cannot.
- Can solve problems involving multiplication, using materials, arrays and repeated addition, or mental methods, and/or multiplication and division facts.
- Can solve problems involving division, using materials, arrays and repeated subtraction, or mental methods, and/or multiplication and division facts.
Year 3:
- Can recall and use multiplication and division facts for the 3, 4 and 8 times tables.
- Can write and calculate mathematical statements for multiplication and division using the multiplication tables that they know, including for 2-digit numbers times 1-digit numbers, using mental methods.
- Can write and calculate mathematical statements for multiplication and division using the multiplication tables that they know, including for 2-digit numbers times 1-digit numbers, using more formal written methods.
- Can solve problems involving multiplication and division.
- Can solve integer scaling problems (e.g. Tommy pays £2 for one ice cream. How much would three ice creams cost?)
- Can solve correspondence problems in which n objects are connected to m objects (e.g. A bag of balls has 2 footballs and 3 rugby balls. Alice bought 2 bags of balls; how many rugby balls did she get?)
- Can solve missing number problems.
Year 4:
- Can recall multiplication and division facts for multiplication tables up to 12 × 12.
- Can use place value, and known and derived facts, to multiply and divide mentally (e.g. knowing 210 ÷ 3 = 70), including multiplying by 0 and 1, and dividing by 1.
- Can multiply together three numbers.
- Can recognise and use factor pairs and commutativity in mental calculations.
- Can multiply 3-digit or 2-digit numbers by a 1-digit number, using a formal written layout.
- Can solve problems involving multiplying and adding, including using the distributive law to multiply 2-digit numbers by 1-digit.
- Can solve integer scaling problems (e.g. Tommy pays £2 for one ice cream. How much would three ice creams cost?)
- Can solve harder correspondence problems such as n objects are connected to m objects (e.g. A bag of balls has 2 footballs and 3 rugby balls. Alice bought 2 bags of balls; how many rugby balls did she get? Amelie bought some bags. She ended up with 10 footballs. How many rugby balls did she have?)
Year 5:
- Can identify multiples and factors, including finding all factor pairs of a number, and common factors of two numbers.
- Knows and uses the vocabulary of prime numbers, prime factors and composite (non-prime) numbers.
- Can establish whether a number up to 100 is prime and recall prime numbers up to 19.
- Can multiply and divide numbers mentally drawing upon known facts.
- Can multiply numbers up to 4-digits by a 1-digit number using a formal written method.
- Can multiply numbers up to 4-digits by a 2-digit number using a formal written method, including long multiplication for 2-digit numbers.
- Can divide numbers up to 4-digits by a 1-digit number using the formal written method of short division.
- Can interpret remainders appropriately for the context when using short division.
- Can multiply and divide whole numbers and those involving decimals by 10, 100 and 1000.
- Can recognise and use square numbers and cube numbers, and the notation for squared (2) and cubed (3).
- Can solve problems involving multiplication and division, including using their knowledge of factors and multiples, squares and cubes.
- Can solve problems involving addition, subtraction, multiplication and division, and a combination of these, including understanding the meaning of the equals sign.
- Can solve problems involving multiplication and division, including scaling by simple fractions and problems involving simple rates.
Year 6:
- Can perform mental calculations, including with mixed operations and large numbers.
- Can multiply multi-digit numbers (up to 4-digits) by a 2-digit whole number using the formal written method of long multiplication.
- Can divide numbers (up to 4-digits) by a 2-digit whole number using the formal written method of long division.
- Can divide numbers (up to 4-digits) by a 2-digit number using the formal written method of short division where appropriate.
- Can interpret remainders as whole number remainders, fractions, or by rounding, as appropriate for the context, when using the formal method of long division.
- Can identify common factors, common multiples and prime numbers.
- Can use their knowledge of the order of operations to carry out calculations involving the four operations.
- Can solve problems involving addition, subtraction, multiplication and division.
- Can use estimation to check answers to calculations and determine, in the context of a problem, levels of accuracy.
Fractions
Year 1:
- Can recognise, find and name a half as one of two equal parts of an object, shape or quantity.
- Can recognise, find and name a quarter as one of four equal parts of an object, shape or quantity.
Year 2:
- Can recognise, find, name and write fractions 1/3, 1/4, 2/4 and 3/4 of a length or a shape, or of a set of objects or a quantity.
- Can write simple fractions e.g. 1/2 of 6 = 3.
- Can recognise the equivalence of 2/4 and 1/2.
Year 3:
- Can count up and down in tenths.
- Can recognise that tenths arise from dividing an object into 10 equal parts and in dividing 1-digit numbers or quantities by 10.
- Can recognise, find and write fractions of a discrete set of objects, both unit fractions (1/5) and non-unit fractions with small denominators (2/5)
- Can recognise and use fractions as numbers: unit fractions and non-unit fractions with small denominators.
- Can recognise and show, using diagrams, equivalent fractions with small denominators.
- Can add and subtract fractions with the same denominator within one whole (e.g. 5/7 + 1/7 = 6/7).
- Can compare and order unit fractions.
- Can compare and order fractions with the same denominators.
- Can solve problems that involve all of the above.
Year 4:
- Can recognise and show, using diagrams, families of common equivalent fractions.
- Can solve problems involving increasingly harder fractions to calculate quantities, and fractions to divide quantities, including non-unit fractions where the answer is a whole number.
- Can add and subtract fractions with the same denominator.
- Can count up and down in hundredths and recognise that hundredths arise when dividing an object by a hundred or by dividing tenths by ten.
- Can recognise and write decimal equivalents of any number of tenths or hundredths.
- Can recognise and write decimal equivalents to 1/4; 1/2; 3/4.
- Can find the effect of dividing a 1- or 2-digit number by 10 and 100, identifying the value of the digits in the answer as units, tenths and hundredths.
- Can round decimals with one decimal place to the nearest whole number.
- Can compare numbers with the same number of decimal places, up to two decimal places.
- Can solve simple measure and money problems involving fractions and decimals to two decimal places.
Year 5:
- Can compare and order fractions whose denominators are all multiples of the same number.
- Can identify, name and write equivalent fractions of a given fraction, represented visually, including tenths and hundredths.
- Can recognise mixed numbers and improper fractions, and convert from one form to the other and write mathematical statements > 1 as a mixed number (e.g. 2/5 + 4/5 = 6/5 = 1 and 1/5).
- Can add and subtract fractions with the same denominator and multiples of the same number.
- Can multiply proper fractions and mixed numbers by whole numbers, supported by materials and diagrams.
- Can read and write decimal numbers as fractions (e.g. 0.71 = 71/100)
- Can recognise and use thousandths, and relate them to tenths, hundredths and decimal equivalents.
- Can round decimals with two decimal places to the nearest whole number, and to one decimal place.Can read, write, order and compare numbers with up to three decimal places.
- Can solve problems involving numbers with up to three decimal places.
- Can recognise the per cent symbol (%) and understand that per cent relates to “number of parts per hundred”, and write percentages as a fraction with denominator hundred, and as a decimal.
- Can solve problems which require knowing percentage and decimal equivalents of 1/2, 1/4, 1/5, 2/5, 4/5 and those with a denominator of a multiple of 10 or 25.
Year 6:
- Can use common factors to simplify fractions and use common multiples to express fractions in the same denomination.
- Can compare and order fractions, including fractions >1.
- Can add and subtract fractions with different denominators and mixed numbers, using the concept of equivalent fractions.
- Can multiply simple pairs of proper fractions, writing the answer in its simplest form (e.g. 1/4 × 1/2 = 1/8).
- Can divide proper fractions by whole numbers (e.g. 1/3 ÷ 2 = 1/6 ).
- Can associate a fraction with division and calculate decimal fraction equivalents (e.g. 0.375) for a simple fraction (e.g. 3/8).
- Can identify the value of each digit to three decimal places, and multiply and divide numbers by 10, 100 and 1000 where the answers are up to three decimal places.
- Can multiply 1-digit numbers (with up to two decimal places) by whole numbers.
- Can use written division methods in cases where the answer has up to two decimal places.
- Can solve problems which require answers to be rounded to specified degrees of accuracy.
- Can recall and use equivalences between simple fractions, decimals and percentages, including in different contexts.
Measurement
Year 1:
- Can compare, describe and solve practical problems for lengths and heights (e.g. long/short, longer/shorter, tall/short, double/half); mass or weight (e.g. heavy/light, heavier than, lighter than); capacity/volume (e.g. full/empty, more than, less than, quarter); and time (e.g. quicker, slower, earlier, later).
- Can measure, and begin to record, length and height, mass/weight, and capacity and volume.
- Can tell the time to the nearest hour and half past the hour, and draw the hands on a clock face to show these times.
- Can measure, and begin to record, the time in hours, minutes and seconds.
- Can sequence events in chronological order, using language such as: before, after, next, first, today, yesterday, tomorrow, morning, afternoon and evening.
- Can recognise and use language relating to dates, including days of the week, weeks, months and years.
- Can recognise and know the value of different denominations of coins and notes.
Year 2:
- Can choose and use appropriate standard units to estimate and measure to the nearest appropriate unit length/height in any direction (m/cm), using rulers; mass (kg/g), using scales; temperature (°C), using thermometers; measure capacity (litres/ml), using measuring vessels. The scales are read in divisions of ones, twos, fives and tens, where all numbers on the scale are given.
- Can compare and order lengths, mass, volume/capacity and record the results using >, < and =
- Can recognise and use symbols for pounds (£) and pence (p).
- Can find different combinations of coins that equal the same amounts of money.
- Can solve simple problems in a practical context involving addition and subtraction of money of the same unit, including giving change.
- Can compare and sequence intervals of time.
- Can tell and write the time to the nearest 15 minutes (using quarter past/to the hour) and draw the hands on a clock face to show these times.
- Can tell and write the time to five minutes and draw the hands on a clock face to show these times.
Year 3:
- Can measure, compare, add and subtract lengths (m/cm/mm), mass (kg/g), and volume/capacity (l/ml).
- Can measure the perimeter of simple 2-D shapes.
- Can add and subtract amounts of money to give change, using both £ and p in practical contexts.
- Can tell and write the time from an analogue clock, including using Roman numerals from I to XII, and 12-hour and 24-hour clocks.
- Can estimate and read time with increasing accuracy to the nearest minute; record and compare time in terms of seconds, minutes, hours and o’clock; use vocabulary such as a.m./p.m., morning, afternoon, noon and midnight.
- Can say the number of seconds in a minute and the number of days in each month, year and leap year.
- Can compare durations of events, for example to calculate the time taken by particular events or tasks.
Year 4:
- Can convert between different units of measure (e.g. kilometre to metre; hour to minute).
- Can measure and calculate the perimeter of a rectilinear figure (including squares) in centimetres and metres.
- Can find the area of rectilinear shapes by counting squares.
- Can estimate, compare and calculate different measures, including money in pounds and pence.Can read, write and convert time between analogue and digital 12 and 24-hour clocks.
- Can solve problems involving converting from hours to minutes; minutes to seconds; years to months; weeks to days.
Year 5:
- Can convert between different units of metric measure (e.g. kilometre and metre; centimetre and metre; centimetre and millimetre; gram and kilogram; litre and millilitre).
- Can understand and use equivalences between metric units and common imperial units, such as inches, pounds and pints.
- Can measure and calculate the perimeter of composite rectilinear shapes in centimetres and metres.
- Can calculate and compare the area of squares and rectangles, including using standard units, square centimetres (cm²) and square metres (m²).
- Can estimate the area of irregular shapes.
- Can estimate volume (e.g. using 1 cm3 blocks to build cubes and cuboids) and capacity (e.g. using water).
- Can solve problems involving converting between units of time.
- Can use all four operations to solve problems involving measure (e.g. length, mass, volume, money) using decimal notation, including scaling.
Year 6:
- Can solve problems involving the calculation and conversion of units of measure, using decimal notation up to three decimal places where appropriate.
- Can use, read, write and convert between standard units, converting measurements of length, mass, volume and time from a smaller unit of measure to a larger unit, and vice versa, using decimal notation to up to three decimal places.
- Can convert between miles and kilometres.
- Can recognise that shapes with the same area can have different perimeters and vice versa.
- Can recognise when it is possible to use formulae for area and volume of shapes.
- Can calculate the area of parallelograms and triangles.
- Can calculate, estimate and compare the volume of cubes and cuboids using standard units, including centimetre cubed (cm³) and cubic metres (m³), and extending to other units such as mm³ and km³.
Geometry – Properties of Shape
Year 1:
- Can recognise and name common 2-D shapes, such as rectangles (including squares), circles and triangles.
- Can recognise and name common 3-D shapes, such as cuboids (including cubes), pyramids and spheres.
Year 2:
- Can identify and describe the properties of 2-D shapes, including the number of sides, and symmetry in a vertical line.
- Can identify and describe the properties of 3-D shapes, including the number of edges, vertices and faces.
- Can identify 2-D shapes on the surface of 3-D shapes, for example a circle on a cylinder and a triangle on a pyramid.
- Can compare and sort common 2-D and 3-D shapes and everyday objects.
Year 3:
- Can draw 2-D shapes and make 3-D shapes using modelling materials.
- Can recognise 3-D shapes in different orientations and describe them.
- Can recognise that angles are a property of shape or a description of a turn.
- Can identify right angles, recognise that two right angles make a half-turn, three make three quarters of a turn and four a complete turn.
- Can identify whether angles are greater than or less than a right angle.
- Can identify horizontal and vertical lines and pairs of perpendicular and parallel lines.
Year 4:
- Can compare and classify geometric shapes, including quadrilaterals and triangles, based on their properties and sizes.
- Can identify acute and obtuse angles.
- Can compare and order angles, up to two right angles, by size.
- Can identify lines of symmetry in 2-D shapes presented in different orientations.
- Can complete a simple symmetric figure with respect to a specific line of symmetry.
Year 5:
- Can identify 3-D shapes, including cubes and other cuboids, from 2-D representations.
- Knows angles are measured in degrees and can estimate and compare acute, obtuse and reflex angles.
- Can draw given angles, and measure them in degrees (°)
- Can identify angles at a point and one whole turn (total 360°); angles at a point on a straight line and ½ a turn (total 180°); other multiples of 90 degrees.
- Can use the properties of rectangles to deduce related facts and find missing lengths and angles.
- Can distinguish between regular and irregular polygons based on reasoning about equal sides and angles.
Year 6:
- Can draw 2-D shapes using given dimensions and angles.
- Can recognise, describe and build simple 3-D shapes, including making nets.
- Can compare and classify geometric shapes based on their properties and sizes and find unknown angles in any triangles, quadrilaterals, and regular polygons.
- Can illustrate and name parts of circles, including radius, diameter and circumference, and know that the diameter is twice the radius.
- Can recognise angles where they meet at a point, are on a straight line, or are vertically opposite, and find missing angles.
Statistics
Year 1:
No objectives.
Year 2:
- Can interpret and construct tally charts, simple pictograms, block diagrams and other simple tables.
- Can ask and answer simple questions by counting the number of objects in each category and sorting the categories by quantity.
- Can ask and answer questions about totalling and comparing categorical data.
Year 3:
- Can interpret and present data using bar charts, pictograms and tables.
- Can solve one-step and two-step questions such as ‘How many more?’ and ‘How many fewer?’ using information presented in scaled bar charts and pictograms and tables.
Year 4:
- Can interpret and present discrete data using appropriate graphical methods, including bar charts.
- Can interpret and present continuous data using appropriate graphical methods, including time graphs.
- Can solve comparison, sum and difference problems using information presented in bar charts, pictograms, tables and other graphs.
Year 5:
- Can solve comparison, sum and difference problems, using information presented in a line graph.
- Can complete, read and interpret information in tables, including timetables.
Year 6:
- Can interpret and construct pie charts and line graphs, and use these to solve problems.
- Can calculate and interpret the mean as an average.
Ratio and Proportion
Year 6:
- Can solve problems involving the relative sizes of two quantities, where missing values can be found by using integer multiplication and division facts.
- Can solve problems involving the calculation of percentages (for example, of measures, and such as find 15% of 360) and the use of percentages for comparison.
- Can solve problems involving similar shapes where the scale factor is known or can be found.
- Can solve problems involving unequal sharing and grouping using knowledge of fractions and multiples.
Algebra
Year 6:
- Can use simple formulae.
- Can generate and describe linear number sequences.
- Can express missing number problems algebraically.
- Can find pairs of numbers that satisfy an equation with two unknowns.
- Can enumerate possibilities of combinations of two variables.
To view this information by year group, select the appropriate document below: